티스토리 뷰
확률밀도함수 : 연속확률변수를 나타내는 함수(특정 확률 변수의 특정 값에서 가지는 크기를 나타내는 함수)
- 즉, 확률 변수가 특정 범위를 가질 때를 나타내는 함수
- ex) 시계 바늘이 0시와 1시 사이에 있을 확률 → 1/12
- probability density function = PDF (확률질량함수 PMF의 연속형 버전)
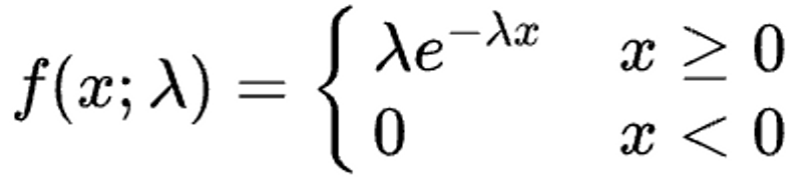
누적분포함수 : 확률 변수가 특정 값보다 작거나 같을 때를 나타냄
- ex) 3시 보다 적을 확률 → 3/12
- Cumulative Distribution Function = CMF

균일분포 Uniform Distribution
분포가 특정 범위(a ≤ x ≤ b) 내에서 균등하게 나타나 있을 경우를 가리키는데,
이 분포는 두 개의 매개변수 a, b를 가지며 [a, b] 내에서 균등한 확률을 가짐

정규분포 Normal Distribution
(= 가우스분포 Gaussian Distribution)
정규분포는 평균과 표준편차가 주어져 있을 때 엔트로피를 최대화하는 분포
(확률이 낮을수록, 어떤 정보일지는 불확실하게 되고, 이때 '정보가 많다'='엔트로피가 높다'고 표현)
표준 정규 분포(standard normal distribution)
X(원점수)를 Z (X-평균) / 표준편차) 로 정규화함으로써 평균이 0, 표준편차가 1인 표준정규분포 N(0,1) 를 얻음

지수분포 Exponential Distribution
사건이 서로 독립적일 때, 일정 시간 동안 발생하는 사건의 횟수가 푸아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기 시간은 지수분포를 따름
이산확률분포인 기하 분포에서 베르누이 시행 횟수(n)이 무한 번이 될 때 지수분포에 수렴
- 푸아송 분포 : 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현
- 기하 분포 : 동일한 베르누이 분포를 따르는 시행의 독립적인 반복에서 첫 성공까지의 시도횟수를 확률변수로 가지는 분포
ex) 1개월에 평균 3회 고장횟수를 가지는 기계에 대해, 수리 후 2개월동안 고장나지 않을 확률
1개월에 3번, 고장나지 않는 개월이 2개월 이상이어야 함
- 확률밀도함수 : 3e^(-3X)
- 누적분포함수 : 1-e^(-3X)
- ⇒ P(X>2) = 1-P(X≤2) = 1-F(2) = 1-(1-e^-6) = 0.0025
참조
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=freepsw&logNo=221193004155
https://blog.naver.com/mykepzzang/220843050893
'데이터분석 > 통계' 카테고리의 다른 글
| 2. 확률과 확률분포_ 표본분포_카이제곱분포 정의 (0) | 2023.08.03 |
|---|---|
| 2. 확률과 확률분포_ 2변수의 확률분포 (0) | 2023.07.31 |
| 2. 확률과 확률분포_ 이산확률분포 (0) | 2023.07.24 |
| 2. 확률과 확률분포_기대치와 분산 (0) | 2023.07.24 |
| 2. 확률과 확률분포_베이즈 정리 / 확률변수 및 확률분포 (0) | 2023.07.02 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 프로그래머스
- leatcode
- 뇌하수체
- 상대도수
- 쿠싱증후군
- Lambda
- 확률
- SQL
- hash
- counter
- 통계
- 뇌하수체선종
- 쿠싱
- 힙
- 파이썬
- 조건부확률
- random forest
- 중앙값
- 확률분포
- 분산
- TensorFlow
- 평균
- 상관관계
- 군고구마
- programmers
- 사분위수
- neural network
- 분당서울대병원
- Python
- 코딩테스트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
