ToDo 머신러닝#1_Ensemble_1/2; 학습 모델 오류 이해

※공부하고 이해한 내용을 나름대로 정리한 포스팅입니다. 

  올바르지 않은 내용이 있을 가능성도 있습니다. 

Ensemble(앙상블)기법이란?_1/2

머신러닝 기법 중 하나인 Ensemble(앙상블)기법이란

샘플링된 각 데이터 셋을 여러 모델들을 통해 학습시킨 후

각 모델의 예측 결과를 집계하여 

더욱 정확한 예측 결과를 뽑아내는 기법을 말합니다.

 

Ensemble기법을 이해하기 위해선,

학습 모델의 예측 오류를 이해하여야 합니다.

Ensemble기법의 목적이 그 오류를 해결하는 것이기 때문입니다.

 

■ 학습 모델의 예측 오류

학습 모델의 예측 오류는 크게

1. Bias(편향)

2. Variance(분산)

으로 나뉘고 이는 각각

under-fitting과 over-fitting로 이어집니다.

(참고; 아래 그림은 회귀와 분류 중, 분류에 해당됨)

참조: https://medium.com/greyatom/what-is-underfitting-and-overfitting-in-machine-learning-and-how-to-deal-with-it-6803a989c76

 

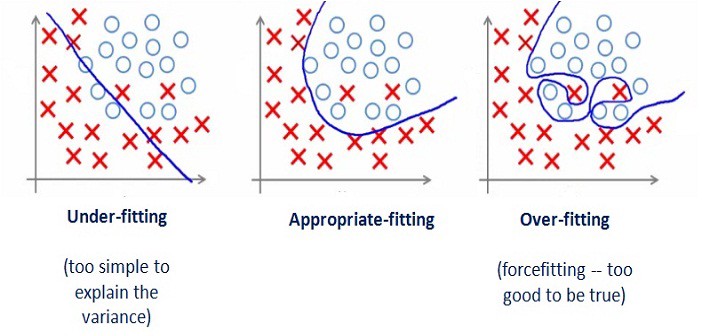
1. Bias

예측값들과 실제 정답의 차이*를 측정합니다.

주로 "제한된 특성"을 가진 예측을 수행할 때 Bias는 높아집니다.

(예: 대한민국 유권자의 투표 결과 예측을 "지역이라는 제한된 변수"로만 수행)

 

높은 Bias를 가진 학습 모델은,

학습 데이터를 충분히 표현하지 못하므로

예측값들이 낮은 정답률을 보이게 됩니다.

 

이러한 모델을 Under-fitting되었다고 합니다.

(=모델의 Complexity 복잡성이 감소함)

 

*참고

수식: f(x)=정답, f^(x)=예측값, E[ ]=기대값=평균

즉, 예측값들의 평균과 실제 정답의 차이를 제곱

참조:  https://www.opentutorials.org/module/3653/22071

2. Variance

각 모델들의 예측값들 간의 차이*를 측정합니다.

주로 "제한된 수"의 표본에서 예측을 수행할 때 Variance는 높아집니다.

(예: 대한민국 유권자의 투표 결과 예측을 "서울이라는 적은 수"의 표본에서만 수행)

 

높은 Variance를 가진 학습 모델은,

학습 데이터셋에 너무 민감하여(=그 학습 데이터셋에만 최적화)

해당 학습 데이터셋에서는 잘 예측할 수 있어도

새로운 데이터 셋에는 잘 작동하지 못하게 됩니다.

 

이러한 모델을 Over-fitting되었다고 합니다.

(=모델의 복잡성이 증가함)

 

*참고

수식: f(x)=정답, f^(x)=예측값, E[ ]=기대값=평균

즉, 각 예측값과 예측값들의 평균간의 차이를 제곱

참조:  https://www.opentutorials.org/module/3653/22071

■ Bias와 Variance의 trade-off

그렇다면,

낮은 Bias와 낮은 Variance를 가지는 모델의

예측값들이 높은 정답률을 보일 것임을 알 수 있습니다. 

 

위의 그림에서도 나타나듯이,

Bias와 Variance가 모두 낮을 때(Low),

예측값(파란 점)들이 정답(빨간 원)에 가까워집니다. 

 

하지만 보통의 경우, 두 오류는

Variance는 낮은데 Bias는 높으며(=모델이 간단함=under-fitting)

Variance는 높지만 Bias는 낮은 (=모델이 복잡함=over-fitting)

Trade-off 관계를 가지고 있습니다. 

이는 모델이 데이터를 반복 학습하는 수(K)를 조정할 때 주로 발생합니다. 

참조: https://stats.stackexchange.com/questions/336433/bias-variance-tradeoff-math

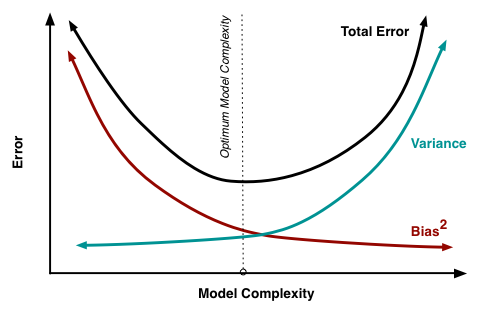
예로, 데이터를 반복 학습시키는 수가 많아지면, (=모델이 점점 복잡해지면)

Bias는 감소하고, 

(= 학습 데이터셋을 반복학습 하다보니 예측값들이 정답을 잘 예측하게 됩니다.)

Variance는 점점 증가합니다.

(= 학습 데이터셋만을 외우다시피 반복하니, 다른 데이터셋은 잘 예측하지 못하게 됩니다.)

 

따라서 모델의 복잡성을 최적화(Optimum Model Complexity)시키는 작업이 필요합니다. 

이는 즉, Total Error*의 최소점을 찾는 것을 의미하고

이 때 Ensemble기법이 적용되게 됩니다. 

 

*참고

Total Error= Bias+Variance+근본적 오차irreducible error

수식: f(x)=정답, f^(x)=예측값, E[ ]=기대값=평균, σ=근본적 오차

참조: https://www.opentutorials.org/module/3653/22071

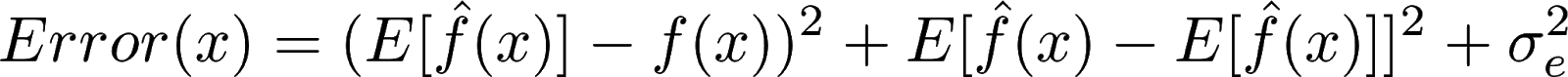
■ Ensemble기법 유형

 

Ensemble기법은 기본적으로 2가지로 나뉩니다.

1. Bagging(배깅)

2. Boosting(부스팅)

 

두 기법 모두 오류(예측값들의 손실)를 최소화하기 위해

약한 분류기(예측값이 정답과 다른 데이터 셋)들을 결합하여

하나의 강한 분류기(실제값과 거의 같은 데이터 셋)을 생성하는 방법이지만,

그 "결합의 방법"에서 차이가 나타납니다.

자세한 내용은 다음 포스팅에서 이어가도록 하겠습니다.

 

참고
1. https://www.slideshare.net/freepsw/boosting-bagging-vs-boosting
2. https://www.opentutorials.org/module/3653/22071